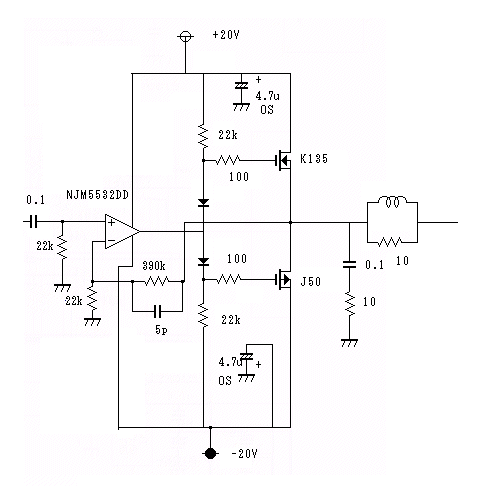
これはK135/J50で構成されるSEPPアンプで電圧増幅段は5532を使っている。技術誌に載ってそうな
回路である。

改めて聴くとこれが音が悪いのである。FE103ペリスコープで聴いているとMOS−FETの良さはところどころに感じ
られるが、聴きづらさがある。リッチでゴージャスな音だがはいりこめない。
この場合技術力でなんとかできるかといえば、そうとも言い切れないところがある。
金田式の音のよさの秘密を探る

これはK135/J50で構成されるSEPPアンプで電圧増幅段は5532を使っている。技術誌に載ってそうな
回路である。

改めて聴くとこれが音が悪いのである。FE103ペリスコープで聴いているとMOS−FETの良さはところどころに感じ
られるが、聴きづらさがある。リッチでゴージャスな音だがはいりこめない。
この場合技術力でなんとかできるかといえば、そうとも言い切れないところがある。
例弊使 I
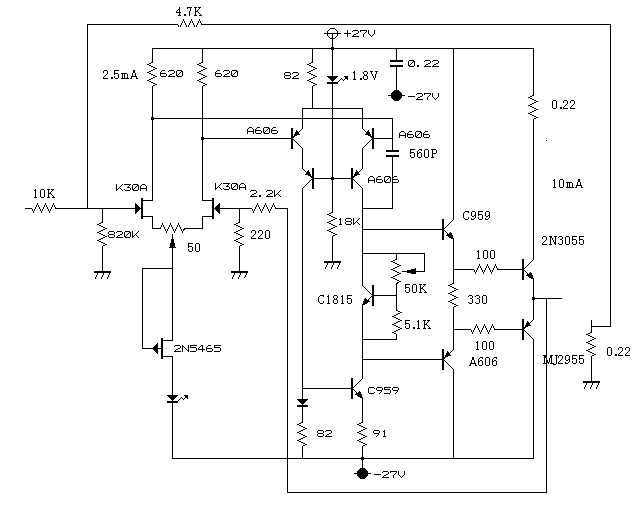

これは金田式にかなり忠実に作れらている。これだと変な表現だが音そのものがきれいで、聴いていて楽しい。MOS
とは違った表現力があり常用アンプにすることができる。
これは一体どういうことなのだろうか。
部品自体が金田氏の耳にかなったものが使われているが、一般化していえば周波数特性が良くて細かい音がでる
デバイスが使われているようである。
同じ部品で上下対称回路にしてみたらどうであろうか。各段で二次歪を抑制する差動回路にくらべ、コンプリ合成では
小信号時の歪率にかなりの差がでそうである。大振幅時では上下対称回路のほうが有利ではある。実働領域では2段差動
回路は直線性が良く、いやな音がでにくい。
2段差動回路に終段V−FETをもってくるとほとんど究極のアンプになると結論付けてよいだろう。
MOS−FETの場合直線性に問題があるため、終段ZDRを併用すると良いのかもしれない。SONY TA−N900
がそういう製品である。
電圧増幅段をオールFET金田式にしてみた。

すざましい透明感。ひんやりと甘い。オールFET独特の世界である。この音は聴き覚えがある(最初に作ったDCアンプ)ので、
当時と同じソースをかけてみた。だいたい再現できているようである。

外国製のFETだと再現できない。少し期待していたが残念。
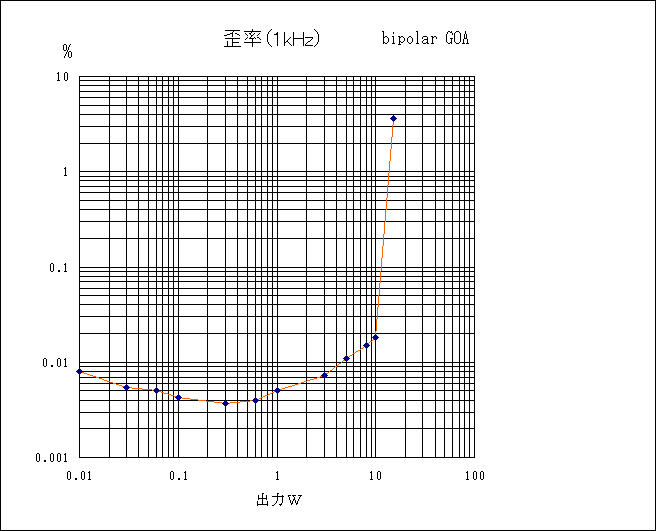
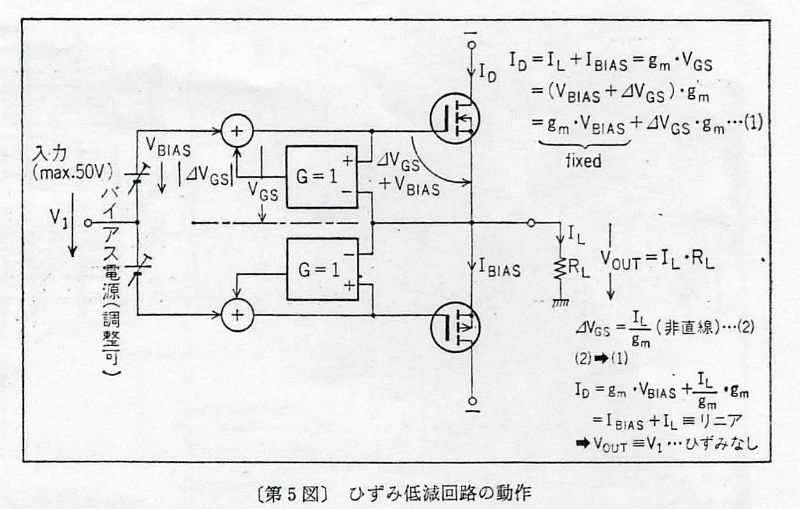
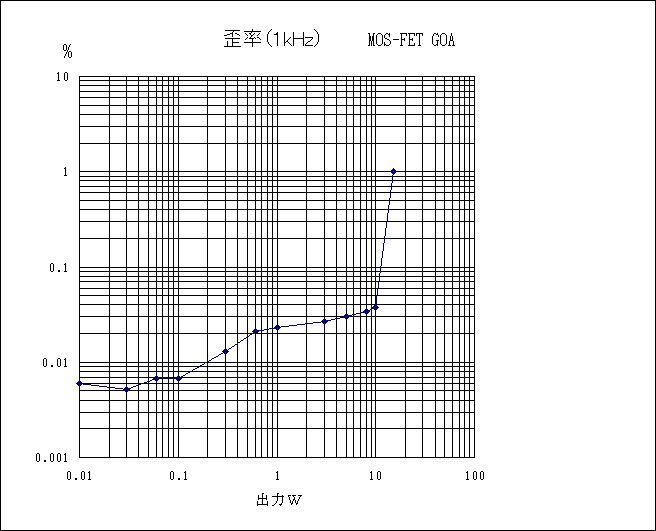
直線性に関しては金田式はこのような状況になっている。(製作記事から引用)
GOAの方が低歪になっていることは間違いない。漸増するカーブは低NFBの特徴である。
踊り場特性は素子及びバイアスの関係によるもの。
エクセルと歪率グラフ
ぺるけ氏の解説を読んでこれは便利だわいと使っていたら、このようなのができてしまった。
簡単な数式が埋め込んであり、デシベルを%に変換してくれる。
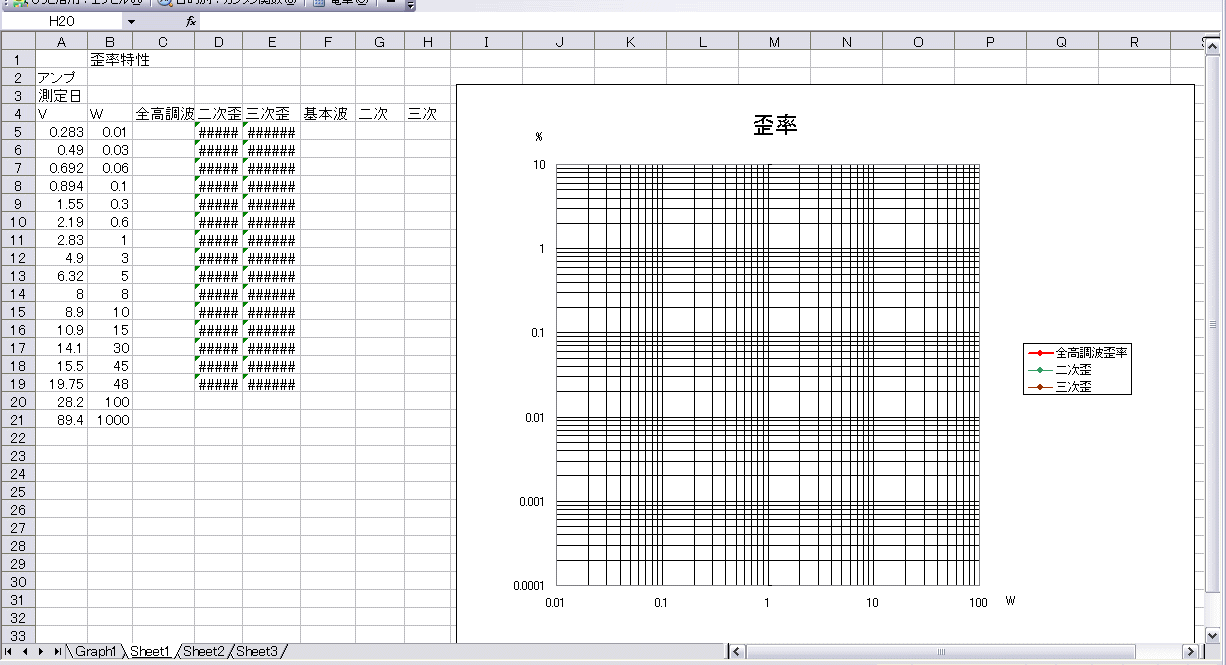
エクセル用参考ファイル
パイオニアA01を測定してみた。
続々 久しぶりにメーカー製アンプを買う
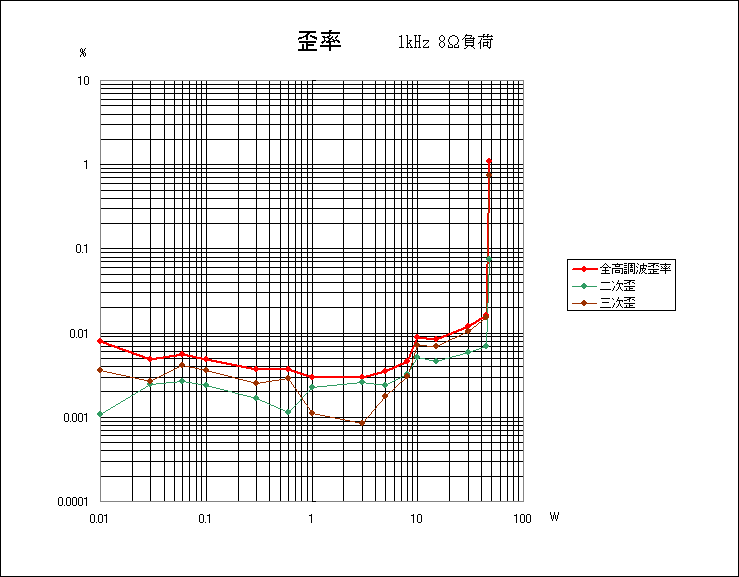
パワーアンプ部はとてもよくできている。NFBが十分かかっており低歪になっている。
いまのはダイレクト入力だったが、ノーマル入力で測定すると次のようになった。
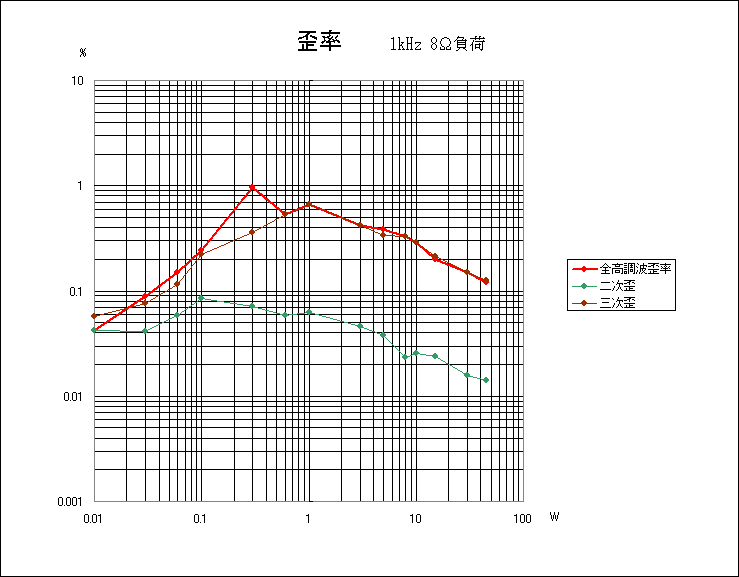
トーンアンプかフラットアンプかどこかでまずいことが起こっていると推測される。
非対称アンプを調べてみた。複合直線素子を用いたシンプルなアンプである。
非対称アンプ「菱垣」
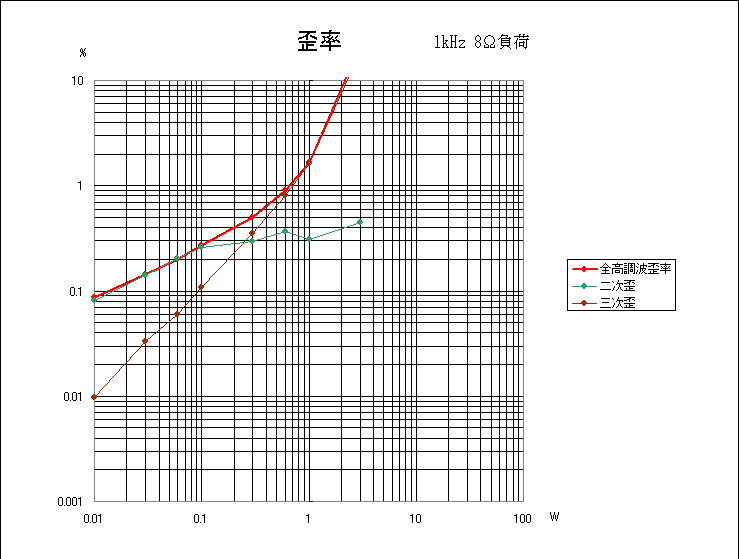
二次歪の部分は透明性を損なわず音楽的な響きをもたらすと考えると、これはとてつもなくいい音がするアンプである
に違いない。実際にそのとうりである。
金田式オールFETGOAを調べてみた。
金田式オールFETパワーアンプ
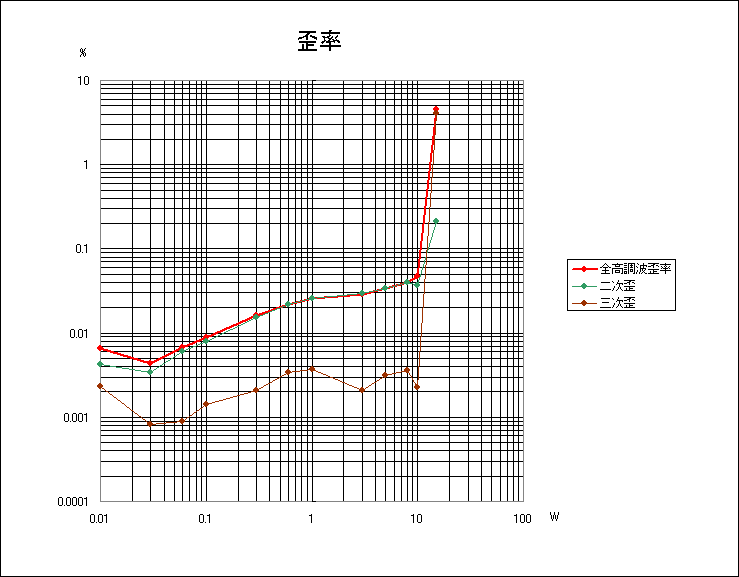
これは夢のようなアンプである。低歪がもたらすクールさ、豊富な2次歪がもたらす甘美な味わいを全域にわたって
楽しめる。
金田式バイポーラGOA
「例弊使」 シリーズ
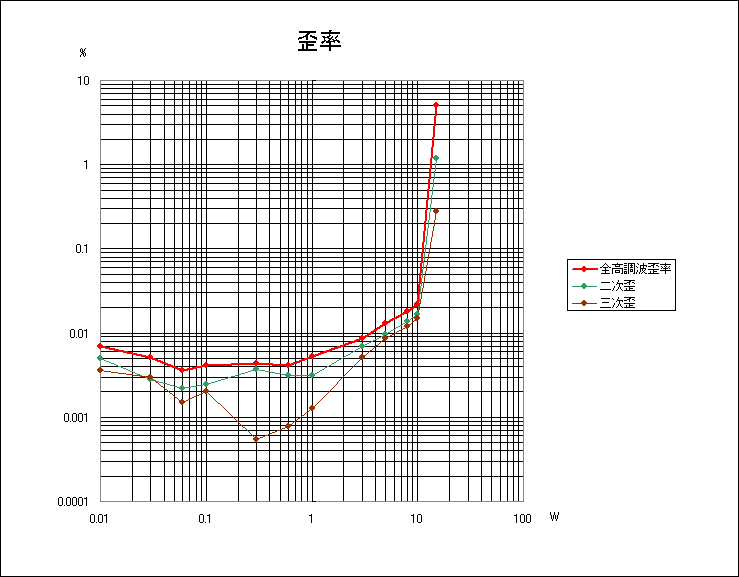
より低歪だが普通のアンプに近い。
N-CHANNEL
POWER MOS FET IRFW I540Aの研究
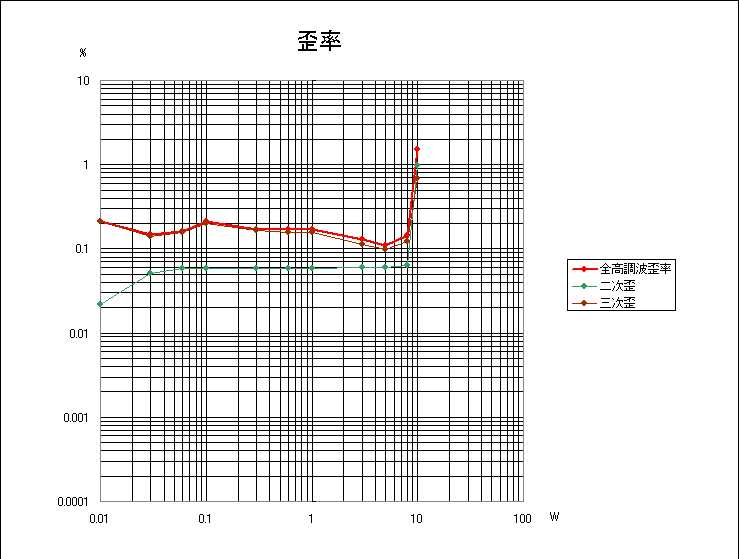
なぜか三次歪が多い。金田式GOAとは音調が異なるのは聴いていてわかる。
自由創作アンプ

天然歪のアンプ。若干二次歪優位。無帰還に近い。
Kabutogani
I
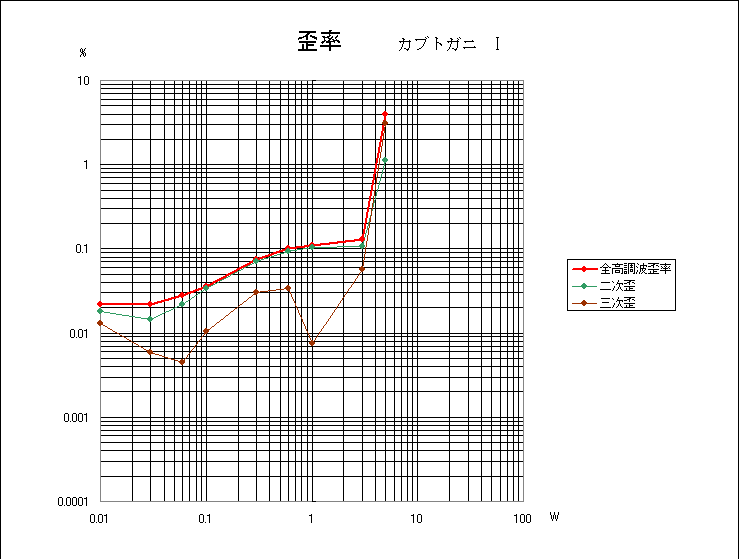
オペアンプによる深いNFBがかけられているが、それでも終段の特性がでている。
非線形アンプの製作
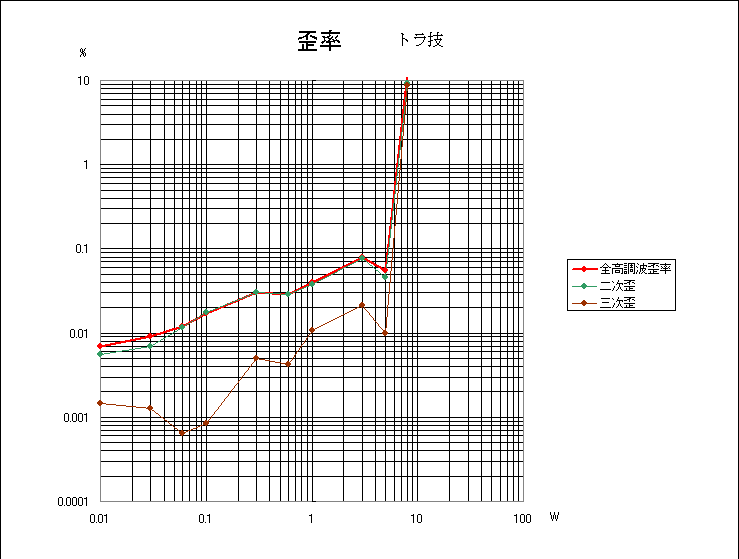
今回は何故か歪が多く出た。この程度のNFBでは終段FETのキャラクターがかなり
残っている。
ディスクリートパワーモジュール V〜XIV

バイポーラ完全対称は3次歪が主体ですね。
詳細

模範的な特性かも。
TRIO KA7300Dを復元する
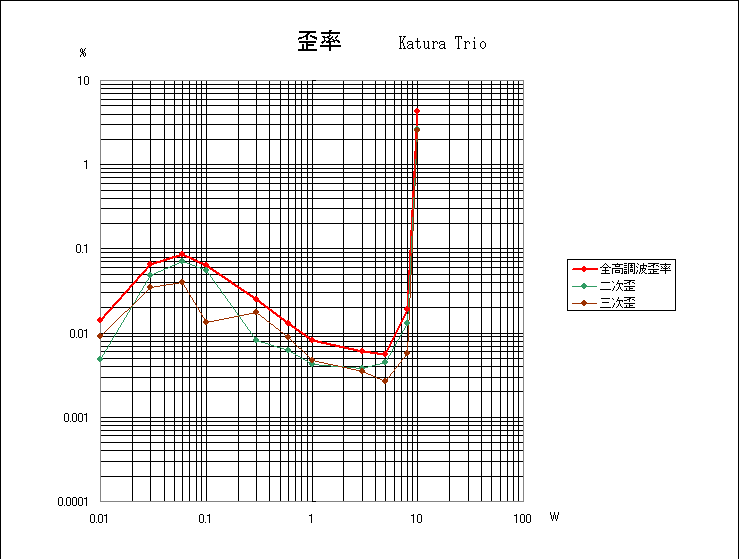
差動三段アンプなので深く帰還がかかっている。
Toshiba K1529/J200 DCパワーアンプ
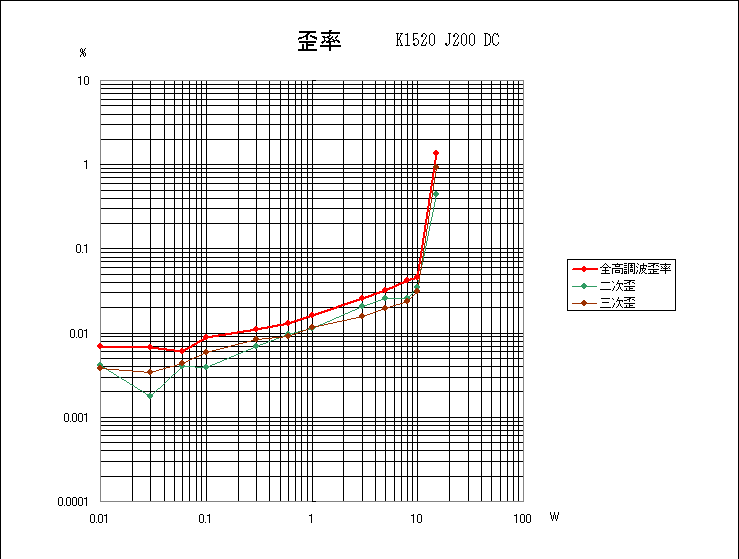
模範的だがMOSらしさは少ないかもしれない。
完全アンプ
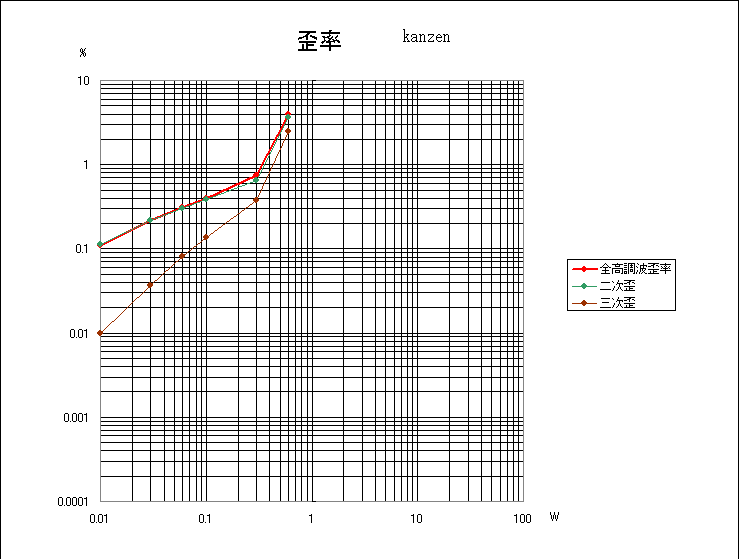
非対称アンプと似た特性(こちらがオリジナルだが)。
6BQ5シングル
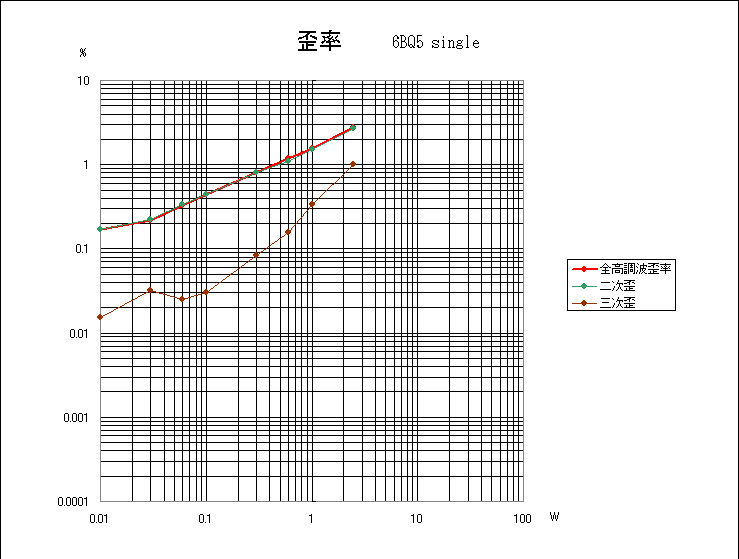
とろけるような音で不思議に思っていたが、やはりこのような特性だった。
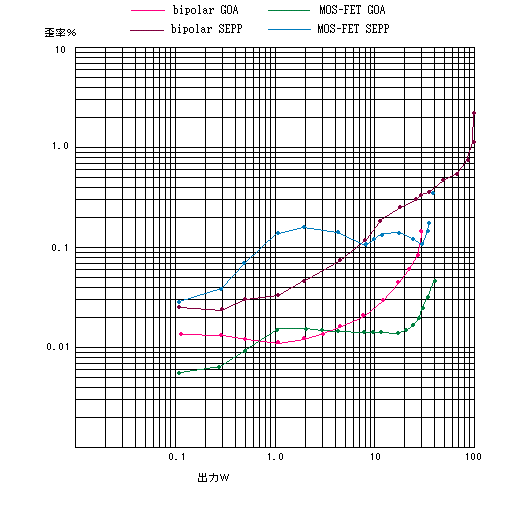
一般的にコンプリ終段の非対称性からくる二次歪や、シングル段の二次歪が主要な歪であるため帰還をかけた状態でも
二次歪が優勢になりやすい。
一方完全対称アンプのように終段の2次歪を対称合成でキャンセルできる回路では、三次歪優勢になるようである。もちろんA級で
なくともプッシュプル合成では、二次歪が三次歪に変換されるので同じことがおこる。(歪変換)
二次、三次とも少ないアンプはたいていNFB過多のアンプである。
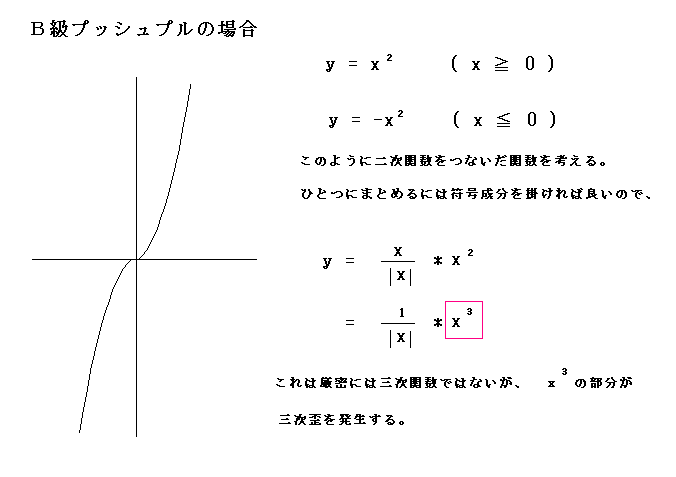
歪変換の原理
二次関数の特性からは二次歪が、三次関数の特性からは三次歪が生ずることを知っていなくてはなりません。(増幅学 I 参照)