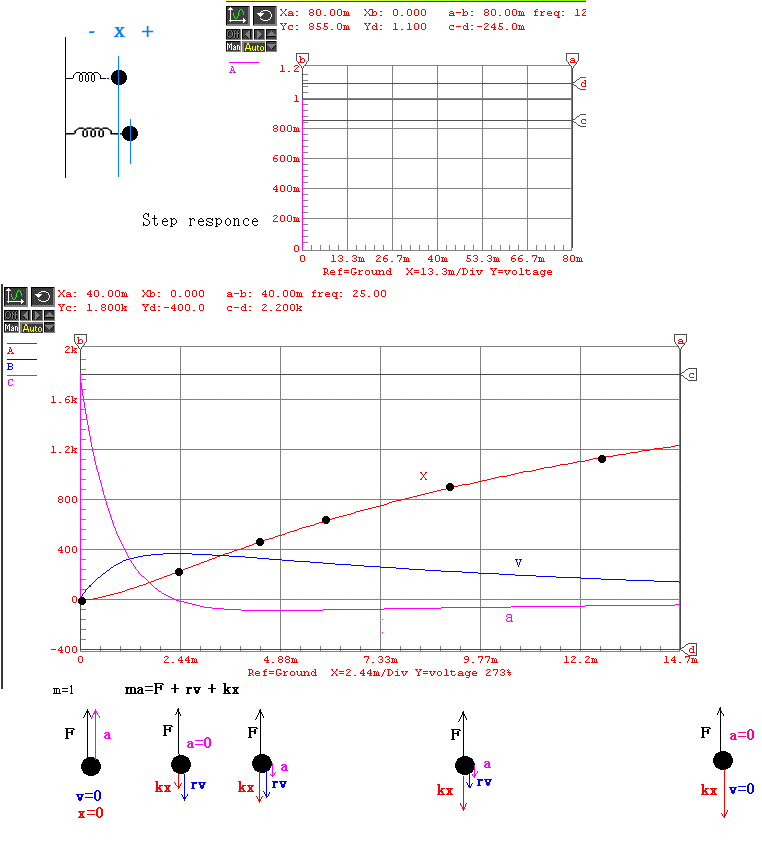
mの質量をもつ物体が加速度aで運動しているとき(あるいは観測されたとき)
物体に加わる力をすべて書くと上記のようになり、これらの力の間にはこのような
関係式が成り立っている(これがニュートンの運動方程式の主張)。
スピーカーでは、mはMoving mass (g)に、kはSuspension compliance (mm/N)
に、 rはSuspension mechanical resistance (Ns/m)に相当する。
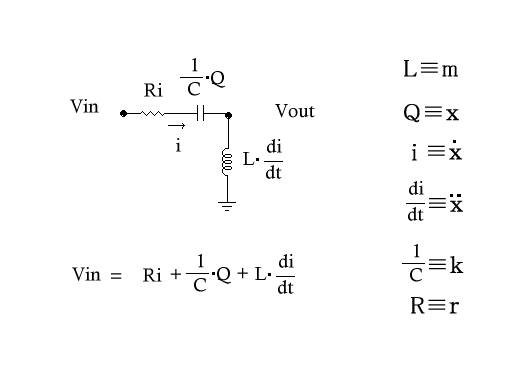
電気量QとキャパシタンスC,インダクタンスLは上記のように微分方程式で
記述でき、しかも力学系の量と一対一で対応しているのでそっくり置き換えて
考えることが可能。
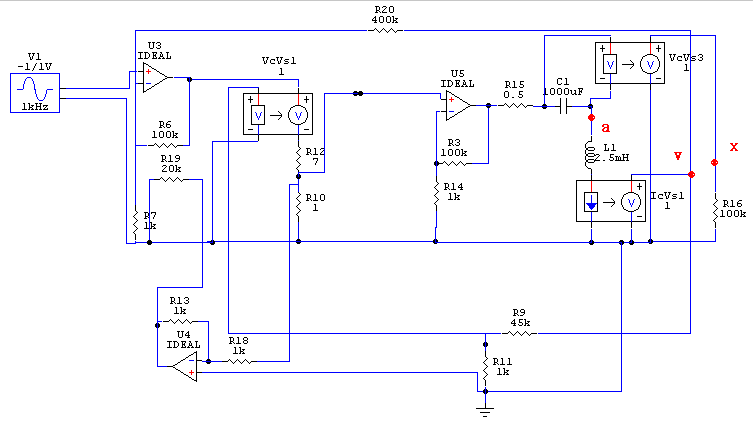
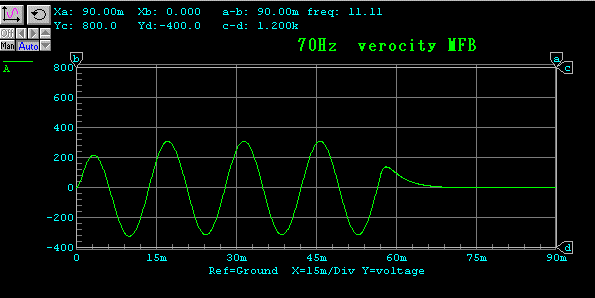
まず速度特性を見ます。電磁制動なしというのは、
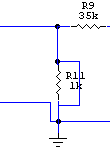
このように電磁制動帰還ループを解除した状態です。電流出力アンプの場合に
相当します。
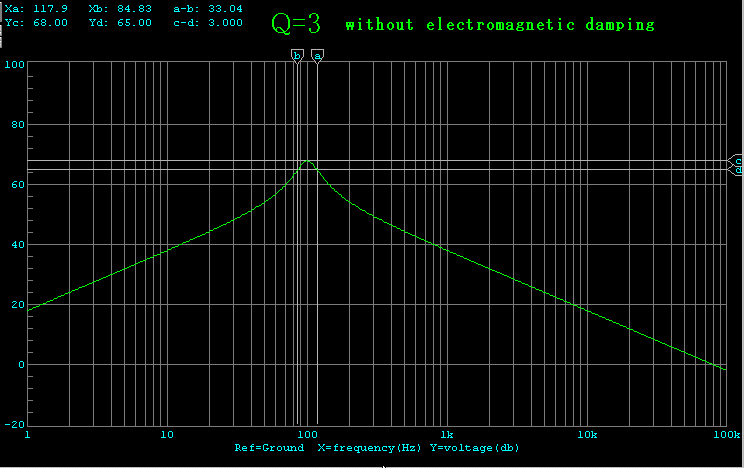
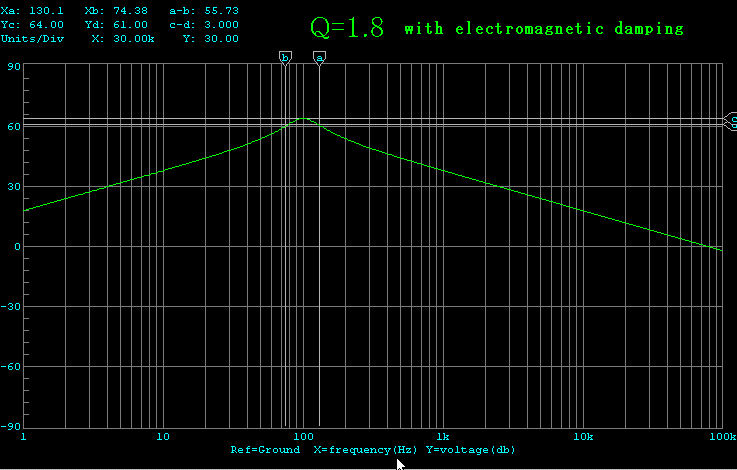
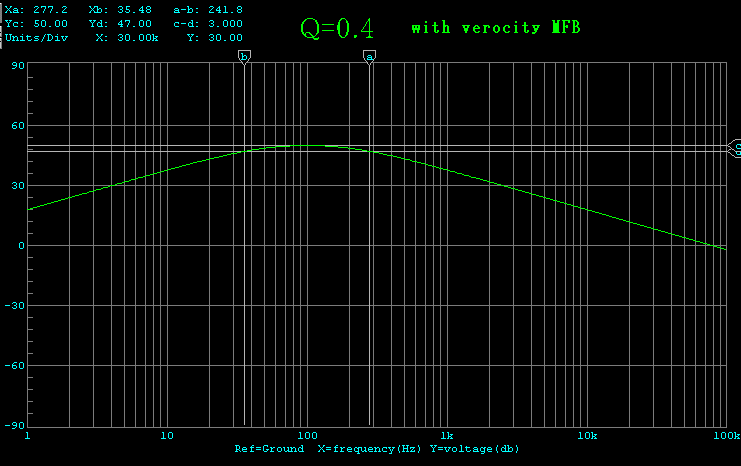
速度特性 黄:電磁制動 緑:速度MFB
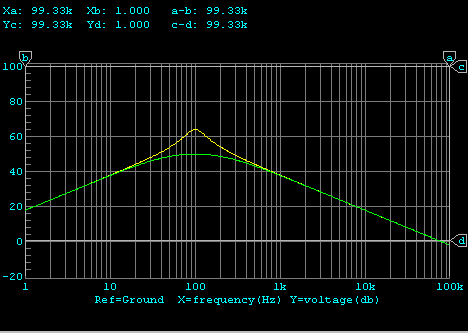
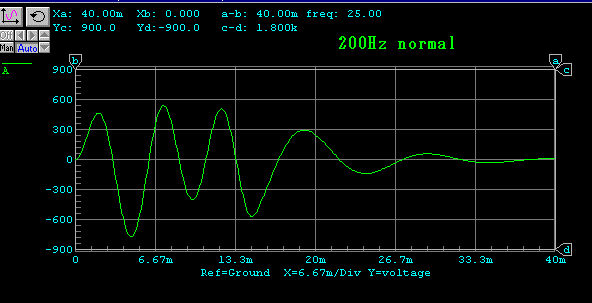
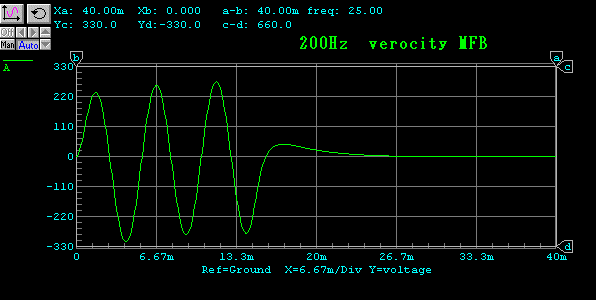
加速度特性 黄:電磁制動 緑:速度MFB
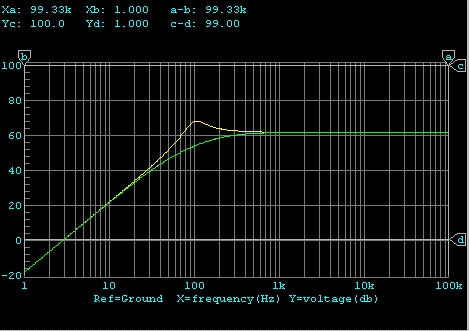
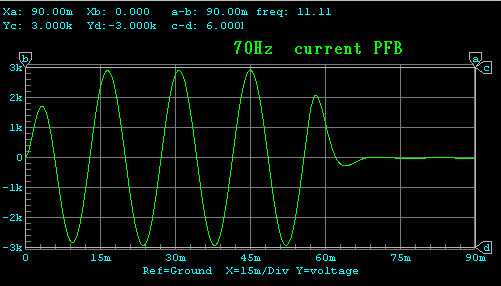
次に、電流正帰還を調べてみます。あまり深く帰還をかけると実機の場合
不安定になるため、帰還は少なめに設定しました。
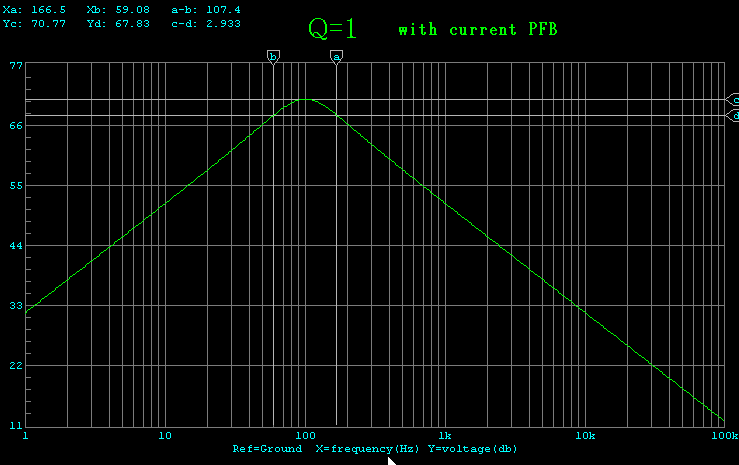
速度特性 黄:電磁制動 緑:電流正帰還
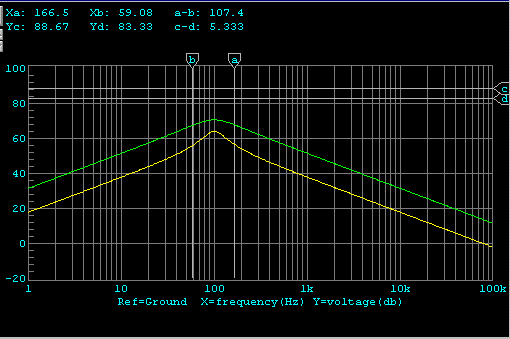
加速度特性 黄:電磁制動 緑:電流正帰還
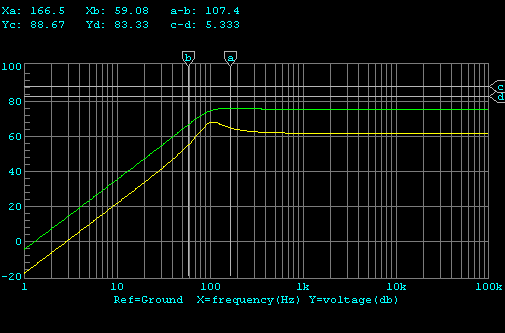
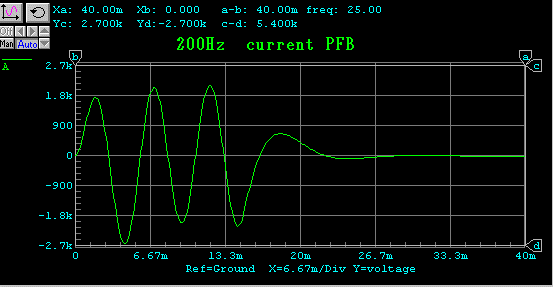
バースト波伝送特性
電気回路でみますと、フィルターの伝達特性となんら変わることがないという
ことがよくわかります。
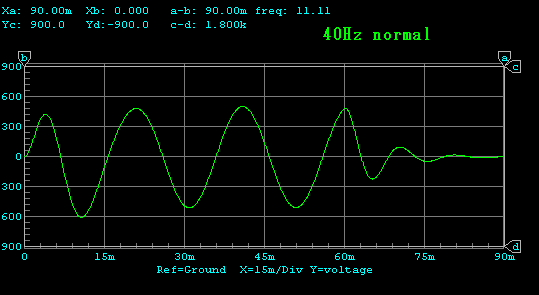
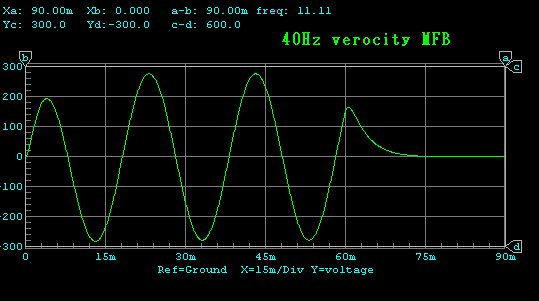
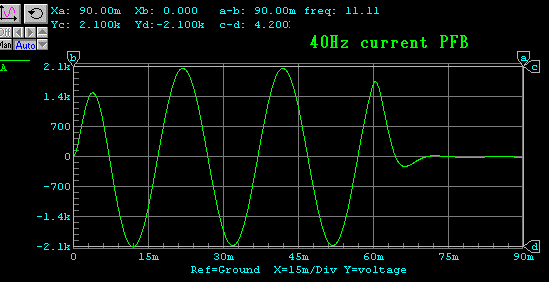
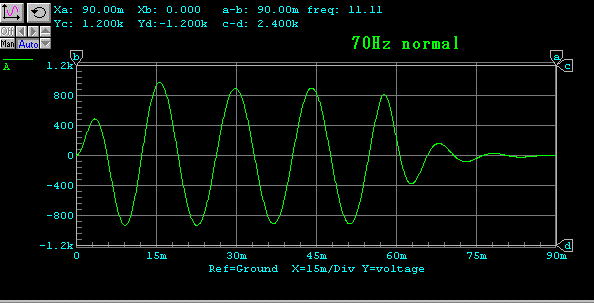
もうひとつ留意すべきことは、速度負帰還を深くかけた場合、入力信号と
速度特性はfsで位相があっており、歪が少なくなるのはいいとして、加速度
特性はどうなるのかという問題です。
答えは、加速度は90°位相が遅れたまま正しい波形になるということで
良いかと思います。